The Measurement of Investment Risk
- World Scholars Review
- Sep 23, 2024
- 27 min read
Updated: Oct 18, 2025

Authors: Matthew Kim & Angelina Zhou
Mentor: Dr. Gerard Dericks (PhD, London School of Economics). Dr. Dericks is currently the director of the Center for Entrepreneurship and Economic Education at Hawaii Pacific University.
Abstract
Asset price volatility has long been established as the leading measure of investment risk, yet has been the subject of continuing criticism due to its internal inconsistencies and historical instances of risk management failure. These shortcomings include demonstrably inaccurate assumptions such as the temporal stability of parameters, the non-normality of return distributions, and material deviation from the concept of risk that business managers and investors customarily adopt. In fact, this review was unable to find a single notable investor who publicly espouses the volatility theory of investment risk. At the same time, a constant stream of alternative risk measures have been put forth in attempt to redress these deficiencies. However, none has been able to fully resolve these weaknesses – many of which are inherent to all metrics that would attempt to quantify future probabilities of asset price behavior with past data. This has led to a lack of consensus among researchers and practitioners as to the most appropriate measure of risk. Perhaps the way forward is through acknowledging the reality that variance and other volatility-based risk metrics can only represent but a singular risk factor within a more multifaceted risk universe, and that the adoption of more holistic and forward-looking approaches to the measurement of investment risk that better align with successful investment and business management practices is needed.
Introduction
Since Markowitz’s (1952) seminal work on portfolio selection over 70 years ago there has been a profusion of related research in mathematical finance. At the core of this field is the use of historical average returns, the variance of these returns, and inter-asset correlations within the context of normal distributions to inform investment decisions. Such metrics are now routinely used by some practitioners and by regulators. For instance, the Basel III global regulatory framework for banks bases required capitalization levels upon Value-At-Risk: a measure of return variance placed within the framework of a normal distribution (Sharma, 2012).
However, there are significant deficiencies in the current operationalization of mathematical finance metrics noted in both the literature and in practical experience. Balbas et al. (2009) for instance report that, “The current literature does not reach a consensus on which risk measures should be used in practice” (p.385), and Byrne and Lee (2004) argue that, “alternative measures of risk have many theoretical and practical advantages” (p.501). These recurrent criticisms have prompted papers across the decades with titles like, “The Limited Relevance of Volatility to Risk” (Kosmicke, 1986), “Risk Is Not The Same as Volatility” (Keppler, 1990), “Risk, Calculable and Incalculable (Dean, 1998), “The Impossible Evaluation of Risk” (Orlean, 2010), and “VAR: Seductive but Dangerous” (Beder, 2019).
Perhaps more importantly, to the authors’ knowledge history’s most successful investors are unanimous in their rejection of the academic interpretation of volatility as a complete summary of investment risk. Its prominent detractors include; Benjamin Graham (Graham and Dodd, 1940, p.101-102), Peter Lynch (Lynch, 1994, 0:12), Michael Burry (Burry, 2000), Mohnish Pabrai (Pabrai, 2022), Jack Bogle (Bogle, 2019), Howard Marks (Marks, 2010), Bill Ackman (Ackman 2012, 13:07), Mark Cuban (Cuban, 2012, 0:56), Charlie Munger (Munger, 2007, 1:38:06), and Warren Buffett (Buffett, 2007, 2:48:40). On the other side of the coin, this review was unable to identify a single proponent of the volatility theory of risk who possesses a distinguished long-term investing track-record. Support for this theory therefore does not seem to extend to those most predisposed to speak on the subject.
Nevertheless, attempts to understand and evaluate risk necessarily form an important baseline for making informed financial decisions. For businesses, being aware of the risks at hand allow them to implement measures to mitigate losses and protect their investments. For investors, risk assessment allows a better understanding of the uncertainty involved with their asset returns, as well as evaluating the likely future performance of their portfolios. Moreover, attempts to quantify risk allows businesses to carry out ‘stress tests’ and circumstantial analyses to assess the robustness and flexibility of an investment strategy.
This paper will continue with a review of the criticisms of standard deviation as a measure of investment risk, survey and critically evaluate alternative risk metrics that have been proposed in its place, and provide a summary and recommendations based on these findings for future risk measurement directions.
Colloquial Definition of 'Risk'
As commonly understood, the word ‘risk’ denotes simply ‘the potential for loss’, or in the words of legendary investor Warren Buffett:
“The likelihood of a permanent loss of investment capital due to deterioration in the underlying performance of the business.”
To many of us this definition seems both intuitive and apposite. But it may come as a surprise to many of us to learn that this is not the definition of risk that has been adopted by scholars of mathematical finance. Instead, their view is that investment risk is completely expressed by the variance - or second moment of the historical investment returns of the asset or portfolio of assets in question. In practice, the square-root of the variance is used, which is known as the standard deviation.
Standard Deviation
Standard deviation is defined as the square root of the mean squared difference (i.e. variance). It is calculated by the formula:

For n total observations of x, where:
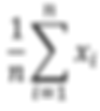
is the mean of the n observations of x
The use of standard deviation as a catch-all measure of risk dates back to work of Samuelson (1970), where he showed that, under certain idealized assumptions about investor utility functions and the properties of asset returns, investors would be exclusively concerned with the mean and variance of returns. By construction, standard deviation will disproportionately weight observations that deviate greatly from the mean according to the square of that difference. In effect, therefore, this measure captures the extent to which an asset’s price moves around in a market, or as Warren Buffet has pejoratively referred to it, an asset’s historical ‘jiggliness’ (Buffett, 2007, 2:50:05).
Criticism
Given that standard deviation deviates substantially from the intuitive understanding of risk, it is not surprising that it has also garnered considerable criticism. We summarize these criticisms in the section below.
1. Backward-looking
“It is difficult to predict, especially the future.”
–Niels Bohr
Firstly, standard deviation is a purely backward-looking metric. Using past price changes to make assumptions about future price direction is inherently problematic, as it ignores dynamic changes in other major factors including the competitive position of the business, its balance sheet, ability to refinance debt, and the regulatory environment. Other popular metrics derived from standard deviation such as VaR also rely on the similarly flawed idea that the future will behave like past history, rendering them unsound approaches to prospective investment (Linsmeier & Pearson, 2000). Risk is always a future prospect and cannot be simply condensed to patterns from the past.
Even Markowitz, the father of mathematical finance warned against only using historical data points to make assumptions about future correlations between assets, which may change. Rather than use past data to mechanically compute asset correlations, he advised investors to use their informed judgment to predict what these correlations are likely to look like in the future, and to calibrate their present portfolios with these subjectively assessed parameters (1952).
2. Volatility is not constant
Patterns of stock market temperament show that volatility is anything but constant. Most of the time markets are relatively stable with a consistent levels of price volatility, however these stable periods are punctuated with episodes of violent adjustments during crises (Ashford, 2023). For instance, in the aftermath of the 2008 financial crisis veteran hedge fund manager George Soros remarked that, “I learned the hard way that range of uncertainty is also uncertain and at times it can become practically infinite” (Soros, 2009). As a result, selecting even slightly differing timeframes from which to analyze volatility can yield drastically different conclusions, emphasizing the inherent instability of this metric (Poon & Granger, 2003). Arguably, it is only in their ability to assess crisis situations that risk measures have any real value. But if a measure consistently breaks down in these crisis scenarios then its utility is questionable.
3. Diversification fails
Using standard division to craft a risk-optimized portfolio encourages excessive diversification by seeking to shrink the total risk down to “beta,” the systemic market risk that cannot be diversified away (Estrada, 2009). However according to many prominent investors, this investment stratagem only ensures mediocre results. Creating high returns with an excessively diversified portfolio proves to be an impossible task, as betting against yourself may limit the downside but equally limits any upside. Many successful investors such as Mark Cuban (2012) do not actively seek diversification to lower volatility. Rather, they see volatility and change as opportunities, and not something to mitigate.
Diversification also relies on the principle that as one asset depreciates, another should appreciate to limit portfolio downside. While this may be true under average market conditions, it is well known that when market crashes occur all asset correlations approach unity, negating the purported benefits of diversification (Loretan and English, 2000). In this way, changing inter-asset correlations render diversification as a risk mitigating strategy ineffectual during a crisis - the very thing diversification is meant to protect portfolios against.
4. Ignores the business
By ignoring the business, underlying factors that are key to valuation such as expected industry growth and the durability of the business’s competitive advantage may be overlooked. Many fundamental value investors like Warren Buffet claim to have been able to achieve consistent above-market returns by focusing on these metrics instead of the business-devoid measures like standard deviation that technical investors assess.
5. Ignores the price
Another key element of risk, or potential for loss that standard deviation ignores is the current asset price. Ceteris paribus, a lower price indicates reduced investment risk as the possible downside is diminished. Additionally, currently undervalued investments may increase substantially in price despite average historical performance, while overvalued companies must do everything right to see the same rates of appreciation continue or even maintain their current price, implying greater riskiness.
6. Returns are not normally distributed
Commonly used risk measures such as standard deviation operate under the assumption that returns are normally and independently distributed and the investor's utility function is quadratic: presumptions that do not hold in practice (Pulley, 1981). Actual stock movements have heavy tails that are not exponentially bounded and display kurtosis (Byrne & Lee, 2004). Because of the “fat tails” of return distributions, other derivations of variance such as VaR (discussed later) also do not accurately reflect the frequency of low-probability loss events and are thus flawed.
7. Lack of universal applicability
Standard deviation becomes inoperable as a measure of risk in any market were assets are not continuously traded. Private businesses, for example, are beyond the reach of this measurement - if the asset isn’t publicly traded, then accordingly its risk cannot be assessed. In markets where asset prices are only infrequently observed, attempts at constructing price indices are equally problematic. In commercial real estate, for instance, the infrequency of transaction data has led to investors using appraisal-based indices in attempt to regularly value their assets (Devaney et al., 2011). Using appraisal-based prices has been criticized for lagging the market, for their inaccuracy, and for ‘smoothing’, which dampens measured volatility compared to a transaction-based price (Cannon & Cole, 2011). By this account, real estate would seem significantly less risky than stocks, when in fact this conclusion is merely an artefact of the reality that comparing the variance between asset prices inside and outside of continuously traded markets is meaningless.
8. Difficult to interpret
It is often said that standard deviation is difficult to understand because its magnitude lacks a clear intuition. This causes investors to consider the volatility of an asset’s returns relative to the volatilities of other assets, rather than its variance in absolute terms, and demonstrates the failure of average investors to grasp the actual magnitude of risk for a given asset (Estrada, 2009). As a consequence, this standard deviation commonly gets confused with other metrics, and creates greater opportunity for an incorrect assessment of the risk involved with an asset’s returns. For instance, mean absolute deviation is a common misconception of standard deviation, a mistake that easily leads investors to underestimate risk anywhere from 25% to 90% of its actual value depending on the actual return distribution shape (Goldstein & Taleb, 2007).
9. Volatility does not necessarily equate to bad outcomes
An ideal risk assessment measure should explicitly focus on downside risks to properly represent the the concept actually of interest to investors (Estrada, 2009). However, volatility as a measure is silent on the likely direction of future asset returns – just because an asset has jiggled around in the past doesn’t necessarily indicate a higher probability of a bad outcome. Standard deviation penalizes both down and up price movements equally, and so fails to favor good companies that may be appreciating in value rapidly, or companies which have precipitously reached a temporary bottom.
Moreover, when risk is associated with volatility, this measure doesn’t take into account the time-frame that the standard deviation of returns is operative. Over the long-term, a more volatile asset such as stocks, is actually a safer bet than a less volatile asset like bonds because, even when negative tail risks do materialize, investors are still more likely to have higher terminal wealth with the historically higher yielding but more volatile asset at the end of the holding period (Dimson et al., 2002, Estrada, 2013). Only highly leveraged investors have reason to fear volatility, a modestly geared long-term investor can disregard bouts of temporary price fluctuations (Estrada, 2013).
10. Historical examples of failure
Perhaps most troubling of all is the empirical failure of risk management strategies utilizing volatility to mitigate investment risk. This was perhaps demonstrated most emphatically with the implosion of Long-Term Capital Management (LTCM). This firm’s board members included the Nobel-Prize-winning economists Myron Scholes and Robert Merton, known for their co-development of the Black-Scholes model for options pricing. While this investment firm operated profitably its first three years, it famously blew up in 1998 because it used mainstream academic finance’s conception of risk. To wit, when asset market volatility exceeded previous bounds in the midst of the late 1997 Asian financial crisis and the early 1998 Russian financial crisis, the firm had to be dissolved and its assets liquidated (Lowenstein, 2001).
Alternative Measures of Investment Risk
Backward-looking Measures 1. Value At Risk (VaR)
Value at Risk is a typical application of standard deviation to measure risk, a statistical measure of possible portfolio loss that has expanded in popularity since it was first pioneered by J.P. Morgan in the 1980s. It has become the standard measure of financial risk since it was sanctioned by the Basel Committee, an entity that serves as risk management practices counsel for financial institutions. Marshall & Siegel (1996) define it as “the expected maximum loss of a portfolio over some time period for some level of probability.” This is typically applied as the maximum potential loss that a portfolio can suffer in the 5% worse cases in 7 days (Acerbi et al., 2018). It is common practice to assume the loss threshold at a 95% confidence level, or a standard deviation of -1.65 in relation to the mean (Thakar, 2022).
VaR’s popularity stems from its ease of use and intuitiveness. It can be applied to any financial instrument, lending high versatility, and is always expressed in the same unit of measure (Acerbi et al., 2001). Although there are many models that can be used to estimate VaR, they all suffer from the major drawback of non-subadditivity, meaning that the actual risk of a portfolio is greater than its summed parts. Additionally, VaR ignores the actual size of defaults (instead only looking at their frequency) by failing to consider extreme price fluctuations, and narrowly focuses on market risk alone (Duffie & Pan, 1997). Perhaps most importantly, VaR operates on the assumption that the future will behave like the past (Linsmeier & Pearson, 2000). All of these criticisms, combined with its non-convexity and the fact it is non-coherent (see Artzner et al., 1997), have led to VaR becoming less viable compared with alternative measures such as Expected Shortfall entering the scene (Cheng et al., 2004).
2. Expected Shortfall/ Conditional VaR/ Expected Tail Loss
Expected Shortfall (ES), also known as Conditional VaR or Expected Tail Loss, has been proposed as a solution to the deficiencies of VaR (Acerbi & Tasche, 2002). Whereas VaR in effect measures the least bad outcome we would expect assuming that we have an unlikely bad outcome, expected shortfall measures the expected value or average loss assuming we have an unlikely bad outcome. This can be expressed as the mean of the 5% worst cases, and thus “ES is the expected value of the loss of the portfolio in the 5% worst cases in 7 days” (Acerbi et al., 2001). Since stock market returns are not normally distributed this distinction may matter, as left-hand tail risks do not decline exponentially, so the magnitude of extreme losses does not get properly factored into VaR.
Expected Shortfall exhibits better properties as a measure of risk than VaR as it can accurately distinguish portfolios which in fact bear different levels of risk. This points out the advantages ES has of being a coherent measure of risk, which means the measurement possesses positive homogeneity, translation invariance, sub-additivity, and monotonicity (TU Delft, n.d.). ES also holds many of the same VaR advantages including it being universal, complete, and simple to understand (Acerbi & Tasche, 2002). While ES is able to account for tail risks, unlike VaR, both VaR and ES are less reliable under market stress (Cheng et al., 2004) and may underestimate low probability catastrophic events (Beus et al., 2003). Furthermore, it is shown by Yamai and Yoshiba (2005) that ES requires larger sets of sample data to reach the same level of precision as VaR. Chabaane et al. (2005) found that optimizing portfolios with ES will yield significantly different results than using VaR, but optimizing with ES constraints proves much faster and more efficient.
Because ES takes into account tail risks, it is able to describe what the unlikely risks entail, while VaR simply gives a probability to expect losses higher than the VaR value itself. It is for this reason that VaR is criticized as an all-or-nothing measure. ES encourages risk diversification, while VaR does not. Finally, it is shown that ES is often easier to approximate than VaR (Dowd, 2002).
3. Semideviation/Lower Partial Moment
Semideviation (Markowitz, 1959) is a measure of the volatility observed below a chosen benchmark, and paved the way for the use of downside risk measures (Estrada, 2008). It is described as the semivariance’s square root, which is equal to the area represented by the downside dispersion space (Ogryczak et al., 1999).
The presence of a risk regularizer and the different choices it allows makes semideviation highly versatile in measuring different riskiness levels. This risk regularizer, while adding to semideviation’s appeal by making it parameterizable, does not satisfy positive homogeneity, or the condition that the risk of a portfolio will remain proportional to its size (Shapiro et al., 2014). However, semideviation can be intuitively adapted as a modification of the mean-variance model; essentially, individuals are looking more at underperformance rather than overperformance. The graphical analysis tool used by Ogryczak et al (1999), O-R (Outcome-Risk) Programs, is easily able to depict this dispersion statistic, as well as many other computerized decision support systems. However, computing the semideviation efficient frontier has proven more difficult than that of the mean variance model, leading it to be less utilized in portfolio optimization (Ogryczak et al., 1999).
Semi-deviation also fails as a measure of risk in the same manner as standard deviation in that big downside moves as a result of market declines that are largely unrelated to the prospects of the business can represent an opportunity to invest, but would similarly count negatively.
4. Mean Absolute Deviation
Mean Absolute Deviation (MAD), proposed by Sharpe (1971) measures the average absolute deviation of portfolio returns from its expected return. This method averages the absolute value of numerous separate errors to determine the precision of a prediction. Like variance, MAD considers a full distribution of returns in measuring risk in portfolios. Under a normal distribution, the portfolio weights for both models are identical, and even when it isn’t, there is no statistically significant difference (Speranza, 1993). But unlike a mean-variance model, MAD doesn’t require computation of the covariance matrix and is less convoluted than Markowitz’s portfolio optimization model. Other properties of MAD that make it preferable to variance include its consistency with the second-order stochastic dominance (Ogryczak et al., 1999). Yitzhaki (1982) notes that MAD demonstrates relatively fewer constraints while still covering the entire distribution of returns for risk measurement.
However, this model tends to assume that asset returns vary in a symmetrical interval, which becomes strongly impractical in commonly seen cases of skewness and extreme market conditions. Attempts to overcome this limit by Li et al. (2006) with forward and backward deviation to vary uncertain asset returns in asymmetrical intervals allow MAD to lose its linearity in minimization, one of its most beneficial advantages.
5. Gain-Loss Spread
The Gain Loss Spread combines three variables: the likelihood of loss, the average magnitude of potential loss, and the average magnitude of potential gain to derive a single expression of possible downside risk. GLS is attractive because it has been shown to correlate highly with standard deviation, which means it provides much of the same information in a more intuitive way and can be looked at in absolute terms, while standard deviation risk measures must be compared relative to other assets. GLS better measures mean return, which would benefit investors who interpret risk as the probability of bad outcomes, not volatility. Finally, GLS is superior to standard deviation in distracting between high and low-risk portfolios, giving more insight into an asset’s risk (Estrada, 2009). Its attempt to asses the potential for gain set it apart from many alternative risk measures, which ignore or discount it.
6. Shortfall Deviation Risk (SDR)
Shortfall Deviation Risk (SDR) combines Expected Shortfall (ES) and Shortfall Deviation (SD - i.e. the spread of results beyond a certain probability). In particular, SDR is defined as the expected loss when that loss exceeds VaR (i.e. ES), which is then penalized by the dispersion of results that represent losses greater than that expectation. a contemplation of the probability of unfavorable events along with an expectation’s variability. Like ES, SDR considers tails, or extreme results, but also penalizes losses higher and lower than ES by dispersion, while simultaneously being less generalized than SD. (Righi & Ceretta, 2015).
Artzner et al. (1999) classifies SDR as a coherent risk measure, satisfying translation invariance, subadditivity, monotonicity, positive homogeneity, strict shortfall and law invariance axioms. SDR’s dual representation builds off theoretical results from the generalized deviation measure SD, to then be combined with the known measure of ES. SDR is suggested to provide greater protection in risk management compared to VaR and ES, specifically in riskier scenarios that allude to more uncertainty. SD’s’ representation of dispersion around an expected value in extreme results creates this elevated protection when ES becomes a correction factor (Righi & Ceretta, 2015).
7. Stable Dispersion Measure
Recognizing that stock market returns not only do not conform to a normal distribution, but may also have variance that is undefined (i.e. infinite) due to fat left-hand tails, these risk models seek to assess risk where variance is undefined but the distribution is nevertheless ‘stable’.
The stable dispersion measure is defined as parametrizing a stable Paretian distribution, under the assumption that returns are in said distribution. This approach was justified by the central limit theorem for independent random variables, as well as the work of Mandelbrot (1963) and Fama (1965) that rejected the normal distribution. Stable modeling, quickly on the rise in finance, allows for kurtosis and skewness, unique characteristics that make this measure a promising candidate (Biglova et al., 2004).
8. Gini Mean Difference
Most commonly seen to measure income inequality and socioeconomic conditions, this method creates an index based on variation of a discrete random variable, using the expected value of the absolute difference between each pair of occurrences (Biglova et al., 2004).
The portfolio selection theory created by Yitzhaki (1982) and Shalit et al. (1984) demonstrates that this approach is consistent with a stochastic dominance rule. Furthermore, the Gini risk measure optimizes portfolios in a linear fashion. This allows simplification of portfolio choice, giving each a concentration curve that makes it easy to identify defensive and aggressive strategies based on the location of the curves (Biglova et al., 2004).
When compared with standard deviation, Gini’s mean difference possesses the same robustness and efficiency under long-tailed distributions for practical purposes. However, this alternative method surpasses standard deviation by lacking SD’s main disadvantage of heavy-tailed distributions, where Gini’s mean difference proves notably more efficient. Furthermore, Gini’s mean difference is unbiased, with a known variance in finite-samples, and allows for better approximative confidence intervals in general (Gerstenberger et al., 2014).
9. Mini-Max
This measure represents the maximum loss over all past observations (Young, 1998). Along with its simplicity and intuitive nature, mini-max has been shown to raise information ratios, lower tracking errors, and improve the performance of optimized robust portfolios. This method has even been shown to be an extreme, unique case of CVar, and therefore satisfies properties of expected tail loss (Biglova et al, 2004).
10. Corporate Solvency Ratings
Corporate solvency ratings have been widely used as a method to evaluate the likelihood of corporate failure (Sen, 1979; Agarwal & Taffler, 2007; Li & Faff, 2019). However, Altman (1968) was among the first to put forward a quantitative model to predict corporate bankruptcy using corporate financial data, and his various Z-score models have been widely applied in industry and academic circles. Although Altman’s Z-score was originally developed as a tool to predict future default, Altman (2002) and others (Sauer, 2002) also advocates that the use of his Z-scores can be extended from bankruptcy prediction to the measurement of corporate financial risk more generally. Nevertheless, Corporate Solvency Ratings such as Z-Scores suffer from the same deficiencies of contemporary relevance as all backward-looking measures, and in practice often their mechanical calculations often yield inconsistent results (Caldecott & Dericks, 2018).
Forward-looking Measures
1. Sustainability of Competitive Advantage
The sustainability of a business's competitive advantage over its competitors, or “moat”, defines the expected consistency of future returns on invested capital. The larger the “moat” is, the less risky a company is to the intelligent investor, a concept highlighted by the likes of Benjamin Graham and his pupil Warren Buffet. Mauboussin and Callahan (2013) detail a systematic framework for analyzing a business's ability to sustain value creation, which can be dissected into two parts: the magnitude of returns a company will generate and the fade rate. By using industry analysis, firm-specific analysis, value-added analysis, management analysis, and brand analysis, an investor may see factors such as a high barrier to entry that implies a sustainable competitive advantage. Companies with a durable competitive advantage are likely to generate superior returns in the future and thus represent low-risk investments. However, given the multifaceted nature of competitive advantage, there can be no consensus on its magnitude and therefore in practice its assessment is necessarily subjective. Moreover, as competitive advantage is dynamic the metric itself will be constantly changing even for the same evaluator.
2. Corporate Bond Ratings
Corporate bond ratings are an independent, professional judgment about of the investment risk associated with a company, looking at the worst possible outcomes in the visible future to predict default probabilities (Schwendiman & Pinches, 1975). While the ‘Big Three’ (S&P, Moody’s, and Fitch) offer different companies rating services, their methodologies are similar and utilize a letter grading system (e.g. Aaa, Aa, A, Baa, Ba, and B).
Corporate bond ratings may give a more complete picture of the investment risk of an individual company because besides taking into account various quantitative factors, it is forward-looking and holistic. Market cyclicality, the impact of foreseeable events, interviews from management, geographic diversification, growth expectations, sector strengths/weaknesses, margins, asset quality, profitability, liquidity, risk management strategies, financial health, debt levels, cash flow, market position, and funding diversity are all taken into account when agencies assign a bond rating (Standard & Poors, 2009). All of these factors, which would otherwise be ignored in backward-looking metrics such as standard deviation, are of key focus to credit agencies, providing a larger context from which investment risk is evaluated from.
A common criticism of the ratings agencies however is their failure to provide accurate risk assessments of mortgage-backed securities prior to the 2008 financial crisis. These agencies, entrusted with evaluating the creditworthiness and risks of financial products, fell short of their responsibilities. Their flawed assessments misled investors, prolonging the boom phase and further exacerbating the depth and severity of the following recession.
Discussion
While standard deviation is customarily used in academic finance as a measure of risk, its conceptual deficiencies and frequent shortcomings in practice means that it is rarely appropriate for measuring risk in financial markets. Our literature review has shown that there exists a great variety of alternative measures still being explored in the world of mathematical risk analysis, demonstrating clear failure to reach a common consensus. However, these proposed alternatives bear many of the same shortcomings such as a reliance on the overly simplistic concept of risk as volatility, backward-looking bias, and ignoring the current price-level of the asset and the business’s competitive position.
The common association of risk measurement with potential loss is an indication that an appropriate measure should explicitly account for future downside risk. The apparent progress being made in mathematical finance is questionable given that practitioners find that not every quantifiable metric is meaningful. In particular, the progress in precision afforded by mathematical finance can lead to a loss in accuracy because a holistic approach to investment risk analysis demands a forward-looking, subjective approach. Because of the necessity for a comprehensive and future-oriented perspective, advancements such as those made by Mauboussin and Callahan (2013) have been particularly insightful in providing an analytical framework to evaluate qualitative business risk factors.
Future research may look to identifying and quantifying what Hillson (2023) calls ‘the multiple dimensions of risk’ (p.1), as well as provide decision criteria for holistically synthesizing their combined values. Methods such as backward testing the importance of factors contributing to the durability of a firm competitive advantage may be used to evaluate the accuracy of proposed models. As is often said, risk, like beauty, is in the eye of the beholder. The biggest challenges going forward will lie in creating a consistent framework that can accurately quantify these factors that will hold across time and space. Although comparatively little work has been done here, informal analyses such as that performed by Bill Gross in his Ted Talk: The Single Biggest Reason Why Start-ups Succeed (2015), and others, are important steps in this more integrative direction.
Conclusion
Although standard deviation is widely used throughout academia, government, and some of professional finance, it differs markedly from how risk is generally conceptualized and exhibits properties that are problematic for a measure of risk. As a backward-looking measure, standard deviation fails to compensate for changing variance and correlations in a dynamic financial environment, and provides negligible diversification benefits in severe market downturns. Standard deviation further assumes a normal distribution as a way of circumscribing risk, when such spreads are rarely accurate in illustrating the distribution of real market asset returns. Additionally standard deviation ignores details about the business, and is unusable for assessing investment risk outside of markets where assets are not continuously traded.
While standard deviation at its basis is a measurement of the dispersion of data points from their mean, many investors and businesses call on risk metrics to focus on solely the downside of their asset returns, or potential losses. An appropriate measure should follow what investors find practically useful, which is often simply an assessment of downside risk relative to the current price. Additionally, standard deviation is difficult for those untrained in statistics to understand and interpret intuitively. This lack of clarity, combined with significant instances of historical failure demonstrate that this metric is less useful in practice than in theory. Without consideration of how the assumptions of standard deviation departs from reality in consequential ways, this risk measure naively treats investments as a physics problem rather than the fundamental business problem that it is.
In response to these shortcomings, many alternative risk measures such as Expected Shortfall, Semideviation, and others have been proposed. However, all of these alternatives likewise have their own deficiencies, many of which they share with standard deviation such as making unrealistic assumptions, as well as being parametric, backward-looking, and non-coherent. The underlying measurement problems that permeate all of the mathematical risk metrics suggest that standard deviation and related metrics of risk should be more generally recognized as but one facet of actual risk instead of an all-encompassing yardstick.
The refinement of more holistic risk measures would perhaps be a positive step forward. Mauboussin and Callahan (2013) outline an analytical context in which to evaluate a business's competitive advantage, serving as a significant benchmark in this area of research. However, such as task will not be easy. Researchers in behavioral finance have argued that, “risk is a concept too complicated to be summarized by a single magnitude, and therefore propose to use not just one but several factors” (Estrada, 2008, p.3). The question then becomes how to quantify that which is inherently subjective, multifaceted, and uncertain. While this represents a fundamental challenge to academic finance, the recognition of these present limitations should serve as a spur for pioneering ways to advance the state-of-the-art in scientific risk measurement.
References
Ackman, W. (2012). William Ackman: Everything You Need to Know about Finance and Investing in under an Hour [Speech video recording. Big Think. https://www.youtube.com/watch?v=WEDIj9JBTC8].
Agarwal, V., & Taffler, R. (2007). Twenty-Five Years of the Taffler Z-Score Model: Does It Really Have Predictive Ability? Accounting and Business Research, 37(4): 285-300.
Altman, E. (1968). Financial Ratios, Discriminant Analysis and the Prediction of Corporate Bankruptcy. The Journal of Finance, 23(4), 589–609. https://doi:10.1111/j.1540-6261.1968.tb00843.x
Altman, E. (2002). Corporate Distress Prediction Models in a Turbulent Economic and Basel II Environment (NYU Working Paper No. S-CDM-02-11).
Artzner, P. (1999). Application of Coherent Risk Measures to Capital Requirements in Insurance. North American Actuarial Journal, 3(2), 11–25. https://doi.org/10.1080/10920277.1999.10595795
Artzner,P., Delbaen,F., Eber, J., & Heath, D. (1997). Thinking Coherently. Risk, 10 ,68-71.
Acerbi, C., Nordio, C., & Sirtori, C. (2001). Expected Shortfall as a Tool for Financial Risk Management. Available at: https://arxiv.org/pdf/cond-mat/0102304
Acerbi, C., & Tasche, D. (2002a). Expected Shortfall: A Natural Coherent Alternative to Value at Risk. Economic Notes, 31(2), 379–388. https://doi.org/10.1111/1468-0300.00091
Acerbi, C., & Tasche, D. (2002b). On the Coherence of Expected Shortfall. Journal of Banking & Finance, 26(7), 1487–1503. https://doi.org/10.1016/s0378-4266(02)00283-2
Ashford, K. (2023, February). What Is Stock Market Volatility? – Forbes Advisor. Available at: https://www.forbes.com/advisor/investing/what-is-volatility/#:~:text=Stock%20prices%20aren
Balbas, A., Garrido, J., and Mayoral, S. (2009). Properties of Distortion Risk Measures. Methodology and Computing in Applied Probability, 11, 385-399.
Beder, T.S. (2019). VAR: Seductive but Dangerous. Financial Analysts Journal, 51(5): 12-24.
Biglova, A., Ortobelli, S., Rachev, S. T., & Stoyanov, S. (2004). Different Approaches to Risk Estimation in Portfolio Theory. The Journal of Portfolio Management, 31(1), 103–112. https://doi.org/10.3905/jpm.2004.443328
Bogle, J. (2019). Jack Bogle: Volatility is NOT Risk [Speech video recording. Investor Talk. https://www.youtube.com/watch?v=AcXTdSL1F7I].
Brutti Righi, M., & Ceretta, P. S. (2016). Shortfall Deviation Risk: An Alternative for Risk Measurement. The Journal of Risk, 19(2), 81–116. https://doi.org/10.21314/jor.2016.349
Buffett, W. (2007). 2007 Berkshire Hathaway Annual Meeting [Speech video recording. Investor Archive. https://www.youtube.com/watch?v=DldvIlHZtKI].
Buffett, W. (2021). Warren Buffett Warns About Diversifying Your Portfolio [Speech video recording. Investor Archive. https://www.youtube.com/watch?v=I9sHKKxXtfc].
Burry, M. (2000). Scion Value Fund, Annual Letter. Available at: http://csinvesting.org/wp-content/uploads/2015/12/BURRY_2000-Annual-Letter.pdf
Byrne, P., & Lee, S. (2004). Different Risk Measures: Different Portfolio Compositions? Journal of Property Investment & Finance, 22(6), 501–511. https://doi.org/10.1108/14635780410569489
Caldecott, B., & Dericks, G. (2018). Empirical Calibration of Climate Policy Using Corporate Solvency: A Case Study of the UK’s Carbon Price Support. Climate Policy, 18(6), 766-780.
Cannon, S., & Cole, R. (2011). How Accurate Are Commerical Real Estate Appraisals? Evidence from 25 Years of NCREIF Sales Data. The Journal of Portfolio Management, 37(1), 68-88.
Chabaane, A., Laurent, J-P., Malevergne, Y., & Turpim, F. (2005). Alternative Risk Measures for Alternative Investments. 1–38. Available at: http://laurent.jeanpaul.free.fr/Alternative_risk_measures_for_alternative_investments.pdf
Cheng, S., Qing Huo Liu, & Wang, S. (2004). Progress in Risk Measurement 1. Advanced Modelling and Optimization, 6(1): 1-20.
Cuban, M. (2012). Cuban on Investing: Diversification is for Idiots [Speech video recording. The Wall Street Journal. https://www.youtube.com/watch?v=u5Pp1HEKSPM&t=553s].
de Bues, P., Bressers, M., & de Graaf, T. (2003). Alternative Investments and Risk Measurement. Proceedings 13th AFIR International Colloquium Maastricht/Niederlande, 1–15.
Dean, M. (1998). Risk, Calculable and Incalculable. Soziale Welt, 49(1): 25-42.
Devaney, S., & Diaz, R. M. (2011). Transaction Based Indices for the UK Commercial Real Estate Market: An Exploration Using IPD Transaction Data. Journal of Property Research, 28(4), 269–289. https://doi.org/10.1080/09599916.2011.601317
Dimson, E., Marsh, P., & Staunton, M. (2002). Triumph of the Optimists – 101 Years of Investment Returns. Princeton University Press.
Dowd, K. (2002). An Introduction to Market Risk Measurement. J. Wiley, New York
Duffie, D., & Pan, J. (1997). An Overview of Value at Risk. The Journal of Derivatives, 4(3), 7–49. https://doi.org/10.3905/jod.1997.407971
Estrada, J. (2009). The Gain-Loss Spread: A New and Intuitive Measure of Risk. Journal of Applied Corporate Finance, 21(4), 104–114. https://doi.org/10.1111/j.1745-6622.2009.00254.x
Estrada, J. (2013). Rethinking Risk. SSRN Electronic Journal. https://doi.org/10.2139/ssrn.2318961
Graham, B. & Dodd, D. (1940). Security Analysis. McGraw-Hill, New York.
Gross, B. (2015). The Single Biggest Reason Why Start-Ups Succeed. www.ted.com. Available at: https://www.ted.com/talks/bill_gross_the_single_biggest_reason_why_start_ups_succeed?language=en
Fama, E. F. (1965). The Behavior of Stock-Market Prices. The Journal of Business, 38(1), 34–105. https://doi.org/10.1086/294743
Gerstenberger, C., & Vogel D. (2015). On the Efficiency of Gini’s Mean Difference. Statistical Methods & Applications, 24: 569-596.
Goldstein, D.G., & Taleb, N.N. (2007). We Don’t Quite Know What We Are Talking about When We Talk about Volatility. Journal of Portfolio Management, 33(4): 84-86.
Hillson, D. (2023) The Risk Management Handbook: A Practical Guide to Managing The Multiple Dimensions of Risk. Kogan Page, London.
Keppler, M. (1990). Risk Is Not The Same as Volatility. Die Bank, 11: 610-614.
Konno, H., & Yamazaki, H. (1991). Mean-Absolute Deviation Portfolio Optimization Model and Its Applications to Tokyo Stock Market. Management Science, 37(5), 519–531. https://doi.org/10.1287/mnsc.37.5.519
Kosmicke, R. (1986). The Limited Relevance of Volatility to Risk. Journal of Portfolio Management, 13(1): 18-20.
Li, X., Balcilar, M., Gupta, R., & Chang, T. (2015). The Causal Relationship Between Economic Policy Uncertainty and Stock Returns in China and India: Evidence from a Bootstrap Rolling Window Approach. Emerging Markets Finance and Trade, 52(3), 674–689. https://doi.org/10.1080/1540496x.2014.998564
Li, L., & Faff, R. (2019). Predicting Corporate Bankruptcy: What Matters? International Review of Economics & Finance, 62, 1-19.
Linsmeier, T. J., & Pearson, N. D. (2000). Value at Risk. Financial Analysts Journal, 56(2), 47–67. https://doi.org/10.2469/faj.v56.n2.2343
Loretan, L., & English W. (2000). Evaluating “Correlation Breakdowns” during Periods of Market Volatility. Federal Reserve System, International Finance Discussion papers.
Lynch, P. (1994). National Press Club Meeting [Speech video recording. The Financial Review. https://www.youtube.com/watch?v=4IhSkIUhjF0].
Mandelbrot, B. (1963). New Methods in Statistical Economics. Journal of Political Economy, 71(5), 421–440. https://doi.org/10.1086/258792
Markowitz, H. (1952). Modern Portfolio Theory. Journal of Finance, 7(11):77–91.
Marks, H. (2010). The Most Important Thing: Uncommon Sense for the Thoughtful Investor. Columbia University Press, New York.
Marshall, C., & Michael Siegel. (1996). Value at Risk: Implementing a Risk Measurement Standard. Working paper, Wharton Financial Institutions Center.
Mauboussin, M. J., & Callahan, D. (2013). Measuring the Moat Assessing the Magnitude and Sustainability of Value Creation. Credit Suisse.
Munger, C. (2007). 2007 Berkshire Hathaway Annual Meeting [Speech video recording. Investor Archive. https://www.youtube.com/watch?v=DldvIlHZtKI].
Ogryczak, W., & Ruszczyński, A. (1999). From Stochastic Dominance to Mean-Risk Models: Semideviations as Risk Measures. European Journal of Operational Research, 116(1), 33–50. https://doi.org/10.1016/s0377-2217(98)00167-2
Orlean, A. (2010). The Impossible Evaluation of Risk. Cournot Centre for Economic Studies. Prisme No. 18.
Pabrai, M. (2022). Look for Low Risk High Uncertainty Businesses – Mohnish Pabrai [Speech video recording. Value Investors Archive. https://www.youtube.com/watch?v=7HkAAJ-a3O8].
Poon, S.H., & Granger, C.W.J. (2003). Forecasting Volatility in Financial Markets: A Review. Journal of Economic Literature, 41(2), 478-539.
Pulley, L. (1981). A general mean-variance approximation to expected utility for short holding periods. Journal of Financial and Quantitative Analysis, 16(3), 361-373.
Samuelson, P. (1970). The Fundamental Approximation Theorem of Portfolio Analysis in Terns of Means, Variances, and Higher Moments. Review of Economic Studies, 37(4), 537-542. https://doi.org/10.2307/2296483
Santos, K. (2009). Corporate Credit Ratings: A Quick Guide. Available at: https://www.treasurers.org/ACTmedia/ITCCMFcorpcreditguide.pdf
Sauer, T. (2002). How may we predict bankruptcy? Business Credit Selected Topic, 104, 16–17.
Schwendiman, C. J., & Pinches, G. E. (1975). An Analysis of Alternative Measures of Investment Risk. The Journal of Finance, 30(1), 193–200. https://doi.org/10.1111/j.1540-6261.1975.tb03170.x
Standard & Poors (2009). Standard & Poor’s Guide to Credit Rating Essentials. S&P Global Ratings. Available at: https://www.spglobal.com/ratings/_division-assets/pdfs/guide_to_credit_rating_essentials_digital.pdf
Sehgal, R., & Jagadesh, P.. (2023). Data-Driven Robust Portfolio Optimization with Semi Mean Absolute Deviation via Support Vector Clustering. 224, 120000–120000. https://doi.org/10.1016/j.eswa.2023.120000
Sen, P.K. (1979). Trend Analysis of Financial Ratios and Forecast of Company Sickness. Decision, 6(1): 97-118.
Shalit, H., & Yitzhaki, S. (1984). Mean-Gini, Portfolio Theory, and the Pricing of Risky Assets. The Journal of Finance, 39(5), 1449–1468. https://doi.org/10.1111/j.1540-6261.1984.tb04917.x
Sharma, M. (2012). Evaluation of Basel III revision of quantitative standards for implementation of internal models of market risk. IIMB Management Review, 24(2), 234-244.
Shapiro, L. A., & Taylor. (2017). The Routledge Handbook of Embodied Cognition. London ; New York: Routledge Taylor & Francis Group.
Sharpe, W. F. (1971). Mean-Absolute-Deviation Characteristic Lines for Securities and Portfolios. 18(2), B-13. https://doi.org/10.1287/mnsc.18.2.b1
Soros, G. (2009). George Soros Open Lecture Series Transcript: Financial Markets. Available at https://www.opensocietyfoundations.org/uploads/2b96bb8c-e2e1-4d88-9eea-badf16d0a2b8/george-soros-financial-markets-transcript.pdf
Speranza, M. Grazia., & Vercellis, C. (1993). Hierarchical Models for Multi-Project Planning and Scheduling. European Journal of Operational Research, 64(2), 312–325. https://doi.org/10.1016/0377-2217(93)90185-p
Thakar, C. (2022, December 9). Value at Risk (VaR) Calculation in Excel and Python. Quantitative Finance & Algo Trading Blog by QuantInsti. https://blog.quantinsti.com/calculating-value-at-risk-in-excel-python/#:~:text=We%20first%20calculate%20the%20mean
TU Delft (n.d.). Coherent Measures of Risk and Back-testing. TU Delft OCW. Retrieved July 15, 2023, from https://ocw.tudelft.nl/course-lectures/3-3-coherent-measures-risk-back-testing/#:~:text=A%20measure%20of%20risk%20is
Yamai, Y., & Yoshiba, T. (2005). Value-At-Risk versus Expected Shortfall: A Practical Perspective. Journal of Banking & Finance, 29(4), 997–1015. https://doi.org/10.1016/j.jbankfin.2004.08.010
Yitzhaki, S. (1983). On an Extension of the Gini Inequality Index. International Economic Review, 24(3), 617. https://doi.org/10.2307/2648789